基因算法解析设计，以背包问题和旅行商问题为例

Posted on | | Visitors:

一、算法说明

基因算法

基因算法有一套公共的完整的框架，伪代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
begin
  set time t = 0 # first generation
  initGeneration() # initialize the population P(t)
  while the termination condition isnot met do
  begin
    
    fitness() # evaluate fitness of each member of the population P(t);
    select() # select members from population P(t) based on fitness;
    
    # produce the offspring of these pairs using genetic operators(cross,mutate);
    # replace candidates of P(t), with these offspring;
    cross() #
    mutate() #
    
    set time t = t + 1 # new generation
  end
end

结合以上代码来分析一下基因算法：

  1. 第3行，首先要初始化第一代种群。这里涉及到一个个体是如何编码的，这一点对于不同的具体问题，要做出不同的实现。
  2. 第4~16行，在终止条件到来之前，种群一代代循环进化，具体如下：
    1. 第7行，计算种群个体的适应度，这里可以评估最优秀个体和平均适应度等。这一点上适应度对于不同的具体问题，其个体适应度计算方法不同，要做出不同实现。
    2. 第8行，根据个体的适应度不同，选出优秀的个体。这一点有多种不同的策略，例如轮盘赌策略和随机二选一的策略。
    3. 12~13行，选出优秀的个体之后，我们要用这些个体产生新一代的种群。具体方法则是交叉和变异。这里有两点需注意，一是交叉或变异的个体的选择有多种不同的策略，二是针对于不同的具体问题，交叉或变异的具体方法不同。
    4. 第15行，经过以上操作产生了新的一代，在这里做出标记。
  3. 当达到终止条件时，则结束进化。

代码设计

根据上述描述分析可以看出，基因算法有一套公用的框架。但有两点值得注意，一是选择，交叉，变异的个体选择有多种不同的策略；二是针对于不同的具体问题，个体的基因编码、交叉和变异的具体方式可能不同。所以在设计框架时，要为这两点留出余地，以便：1. 方便复用代码扩展新策略的基因算法，2. 复用代码实现针对于具体问题的基因算法。

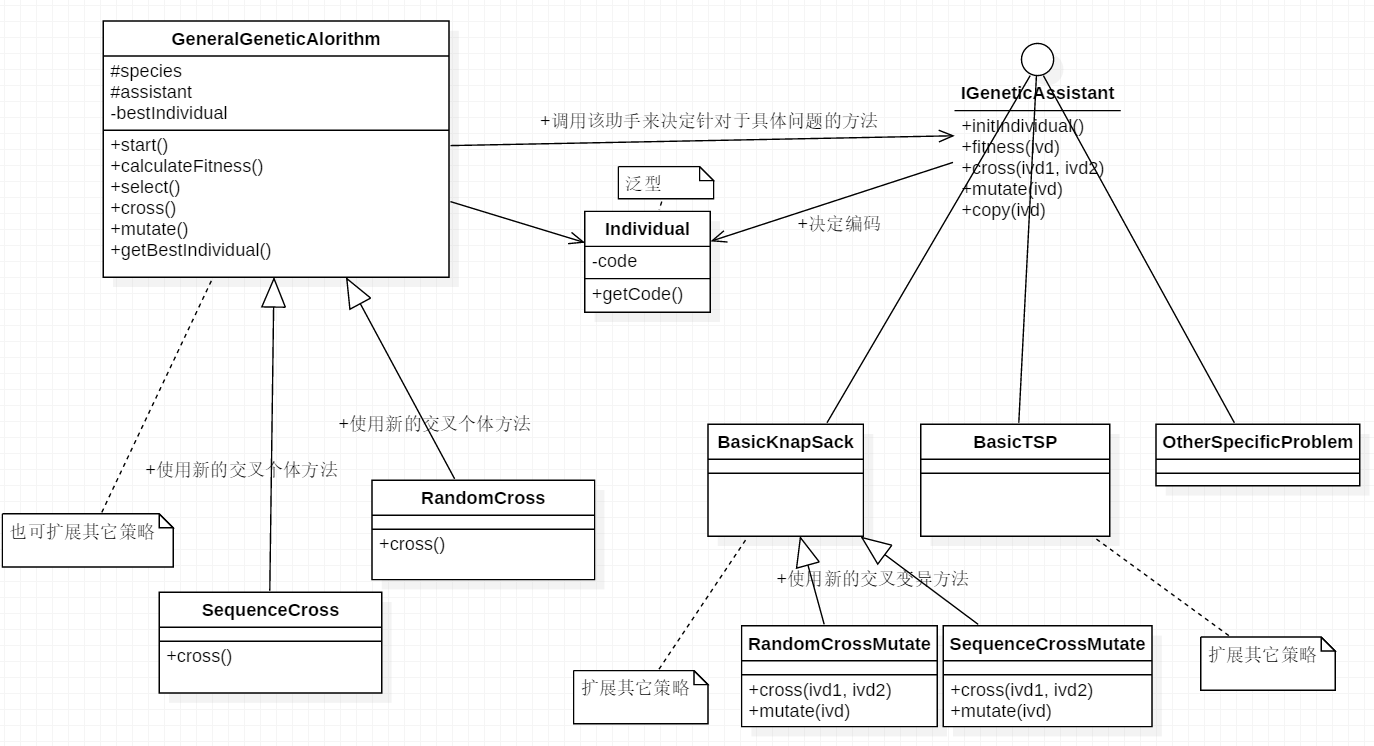
设计图如下：

基因算法设计图

如设计图所示，GeneralGeneticAlgorithm已经实现了基因算法的基本框架，选择，交叉，变异的个体选择都有默认实现。

1
2
3
其默认的选择个体的策略时轮盘赌的策略。
默认的交叉是以一定概率挨个询问个体是否交叉，凑够两个时将两个个体进行交叉。
默认的变异是以一定概率挨个询问个体是否要变异。

其次使用该框架时，必须传入一个继承IGeneticAssistant接口的assistant，assistant决定个体的编码，交叉和变异方式。

使用如下：

1
2
3
4
5
6
7
8
9
IGeneticAssistant assistant = new BasicKnapSack(); //以背包问题为例
GeneralGeneticAlgorithm algorithm = 
			new GeneralGeneticAlgorithm(iterationMax, scale,
			assistant, crossP, mutateP);//其他参数是迭代次数，种群规模，交叉概率，变异概率

algorithm.start(true); //调用此函数开始迭代，true表示迭代过程中打印出每代信息

// 结束后可以取出最好的个体
System.out.println(algorithm.getBestIndividual().toString());

然后也可以继承GeneralGeneticAlgorithm复用代码来实现新策略的基因算法，如图SequenceCross和RandomCross都是复写了父类cross算法，采用不通的策略来选择要交叉的个体。

背包问题

这时候解决背包问题就简单了，只要实现IGeneticAssistant决定个体的编码，适应度评估，交叉，变异和拷贝方式。如上设计图所示的BasicKnapsack类采用如下具体设计。

  1. 个体编码：用一个byte数组表示DNA，个体DNA的长度就是所有物品的数目，然后每一个位置的基因设置为0或1，表示不拿或拿当前的物品
  2. 适应度评估：评估方式很简单，就是将选择的个体的价值都加起来，作为适应度；但如果其总重量超过背包容量，就将其适应度置为0（为防止小概率的种群总适应度为0的情况，可以将此适应度置为接近0，如1e-10）
  3. 交叉：交叉方式是随机选一个起点和终点，然后将两个个体在起点和终点之间的基因段进行交换。
  4. 变异：变异方式是随机选一个起点和终点，然后将该个体在起点和终点之间的基因段中0变1，1变0
  5. 拷贝：由于编码采用数组，所以复制产生新个体时，要将数组中每个值都拷贝一份，才能避免使用相同地址空间。

然后设计图中RandomCrossMute复写交叉和变异的方法：

  1. 交叉：随机生成要改变基因数，然后挑选随机位置的基因进行互换。
  2. 变异：随机生成要改变基因数，然后挑选随机位置的基因0，1倒置。

设计图中的SequenceCrossMute顾名思义就是沿用了默认的方法，将其单独写出来，只是使得结构清新一点。

扩展其它策略的便签是指也可以继承BasicKnapsack来复写特定方法更改策略。

旅行商问题

旅行商问题也是要实现IGeneticAssistant决定个体的编码，评估，交叉，变异和拷贝方式。如上设计图所示的BasicTSP类采用如下具体设计(首先将所有地点存在一个数组里)。

  1. 个体编码：用一个int数组表示DNA，DNA是地点访问顺序的一个序列，也就地点数组下标的一个序列。

  2. 适应度评估：首先计算出旅行商按该个体DNA序列出发再回到起点的总路程，取其倒数作为适应度。也就是距离越短适应度越高

  3. 交叉：交叉的方式比教复杂，举个列子：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    // 这是为交叉之前的两个DNA序列，先随机选取两个点将其分成三份。
    p1 = ( 1 9 2 | 4 6 5 7 | 8 3 )
    p2 = ( 4 5 9 | 1 8 7 6 | 2 3 )
    // 然后将p2从第三部分开始得到临时的新序列tmp2
    tmp2 = 2 3 4 5 9 1 8 7 6
    // 这时候p1的三部分中的中间那部分（记为p12）保持不动，
    // 然后将第一部分和第三部分依此用tmp2中不在p12区间内的元素替换
    // 然后就可以得到p1交叉后的结果c2
    c1 = ( 2 3 9 | 4 6 5 7 | 1 8 )
    // 同样，也可以得到p2交叉后的c2
    c2 = ( 3 9 2 | 1 8 7 6 | 4 5 )

  4. 变异：变异比较简单，举个列子：

    1
    2
    3
    4
    // 同样将待变异p1随机分成三部分
    p1 = ( 1 9 2 | 4 6 5 7 | 8 3 )
    // 然后将中间部分颠倒顺序就得到变异后的c1
    c1 = ( 1 9 2 | 7 5 6 4 | 8 3 )

  5. 拷贝：由于编码采用数组，所以复制产生新个体时，要将数组中每个值都拷贝一份，才能避免使用相同地址空间。

最后扩展其它策略的便签是指也可以继承BasicTSP来复写特定方法更改策略，我没有实现其它策略。

二、背包问题实验分析

实验设计

1
2
3
4
5
6
7
8
9
10
11
12
static double[] mutatePs = {0.05,0.1,0.15,0.2,0.3,0.5,0.8};
static double[] crossPs = {0.3,0.5,0.7,0.85};
static int[] scales = {500,1000,1500};

for (int i = 0; i < crossPs.length; i++) {
     for (int j = 0; j < mutatePs.length; j++) {
       for (int j2 = 0; j2 < scales.length; j2++) {
         doTrain(crossPs[i], mutatePs[j],
                 scales[j2], 10000);
       }
     }
}

实验设计就像如上代码所示，分别以一定的区间来跑完所有的测试，然后将每组测试输入的到对应的文件中。实验跑完之后，对实验结果进行分析，然后缩小区间再进行实验。

实验输出模式

实验过程中每隔300代输出一次，模式如下：

1
2
// 当前代数，当前代最佳适应度，当前代平均适应度，所有代中最佳适应度
g: 9901,best: 106.29999999999998,average: 82.61720000001445,best in total: 106.29999999999998

最终会输出最佳个体，以及最佳个体最早出现的代数

1
2
// 代数：适应度，个体编码
351:106.29999999999998,0 1 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 0 1 0 0 0 0 0 1

实验结果分析

实验结果从以下角度来衡量

  1. 最佳个体适应度：参数优良性
  2. 最佳个体最早出现代数：收敛速度
  3. 最终几代最佳适应度和平均适应度：参数对种群特征的影响。

实验参数会从种群规模，交叉概率，变异概率，交叉变异算法来分析，实验结果见附件部分，具体分析如下

以下结果默认是随机选择交叉个体，具体的交叉变异方法是连续一段的交叉变异。

  1. 种群规模影响

    | 实验序号 | 交叉概率 | 变异概率 | 种群规模 | 最佳最早出现代数 | 最佳个体适应度 | 最终代最高/平均适应度 |
    | :——: | :——: | :——: | :——: | :————–: | :————: | :——————-: |
    | 1 | 0.3 | 0.05 | 1000 | 4985 | 101.39 | 96.599/91.689 |
    | 2 | 0.3 | 0.05 | 1500 | 6039 | 104.69 | 102.99/98.249 |
    | 3 | 0.3 | 0.05 | 500 | 7199 | 103.29 | 99.399/95.099 |
    | 4 | 0.3 | 0.15 | 1000 | 5167 | 104.69 | 103.39/88.305 |
    | 5 | 0.3 | 0.15 | 1500 | 2543 | 106.29 | 104.69/87.514 |
    | 6 | 0.3 | 0.15 | 500 | 5384 | 106.29 | 104.79/85.406 |
    | 16 | 0.3 | 0.5 | 1000 | 4934 | 106.29 | 101.69/56.033 |
    | 17 | 0.3 | 0.5 | 1500 | 1759 | 106.29 | 102.49/55.495 |
    | 18 | 0.3 | 0.5 | 500 | 5568 | 106.29 | 99.699/58.009 |
    | 19 | 0.3 | 0.8 | 1000 | 8131 | 103.39 | 93.5/39.687 |
    | 20 | 0.3 | 0.8 | 1500 | 2565 | 106.29 | 95.399/38.583 |
    | 21 | 0.3 | 0.8 | 500 | 4590 | 102.89 | 88.099/39.505 |

    从以上数据每三组对比分析，可得

    1. 种群规模较大的1500每次都取得最好的结果，而且除了第1、2、3组之外其它都是种群规模大的更快得到最优的个体。
    2. 但是种群规模大会导致训练速度变慢。

  2. 交叉变异概率的影响

    | 实验序号 | 交叉概率 | 变异概率 | 种群规模 | 最佳最早出现代数 | 最佳个体适应度 | 最终代最高/平均适应度 |
    | :——: | :——: | :——: | :——: | :————–: | :————: | :——————-: |
    | 1 | 0.3 | 0.05 | 1000 | 4985 | 101.39 | 96.599/91.689 |
    | 2 | 0.3 | 0.05 | 1500 | 6039 | 104.69 | 102.99/98.249 |
    | 3 | 0.3 | 0.05 | 500 | 7199 | 103.29 | 99.399/95.099 |
    | 19 | 0.3 | 0.8 | 1000 | 8131 | 103.39 | 93.5,a/39.687 |
    | 20 | 0.3 | 0.8 | 1500 | 2565 | 106.29 | 95.399/38.583 |
    | 21 | 0.3 | 0.8 | 500 | 4590 | 102.89 | 88.099/39.505 |
    | 22 | 0.5 | 0.05 | 1000 | 4222 | 106.29 | 103.99/98.414 |
    | 23 | 0.5 | 0.05 | 1500 | 0 | 1.0E-1 | 1.0E-1/9.9999 |
    | 24 | 0.5 | 0.05 | 500 | 0 | 1.0E-1 | 1.0E-1/1.0000 |
    | 43 | 0.7 | 0.05 | 1000 | 0 | 1.0E-1 | 1.0E-1/9.9999 |
    | 44 | 0.7 | 0.05 | 1500 | 0 | 1.0E-1 | 1.0E-1/9.9999 |
    | 45 | 0.7 | 0.05 | 500 | 0 | 1.0E-1 | 1.0E-1/1.0000 |
    | 73 | 0.85 | 0.2 | 1000 | 3235 | 106.29 | 106.29/82.733 |
    | 74 | 0.85 | 0.2 | 1500 | 351 | 106.29 | 106.29/82.617 |
    | 75 | 0.85 | 0.2 | 500 | 0 | 1.0E-1 | 1.0E-1/1.0000 |
    | 76 | 0.85 | 0.3 | 1000 | 569 | 106.29 | 104.79/69.521 |
    | 77 | 0.85 | 0.3 | 1500 | 386 | 106.29 | 104.59/71.282 |
    | 78 | 0.85 | 0.3 | 500 | 6896 | 106.29 | 104.79/72.296 |
    | 79 | 0.85 | 0.5 | 1000 | 2752 | 106.29 | 103.09/56.570 |
    | 80 | 0.85 | 0.5 | 1500 | 340 | 106.29 | 101.89/56.360 |
    | 81 | 0.85 | 0.5 | 500 | 6702 | 106.29 | 94.599/54.731 |

    根据以上数据，可以看出交叉变异会严重影响种群，有以下几点

    1. 由于初始值是随机二选一，平均会选一半物品，导致一般一开始都会超过背包容积，这时，如果变异概率很小，会导致种群难以进化，根据上表，可以看到这一点再种群规模小，交叉概率大的时候更加显著。

    2. 交叉变异的概率增大，会使得种群的收敛速度变快，种群1500的基础上，上表74、77、80都是在500次以内收敛，而交叉变异概率小的3、20则收敛较慢。3和20内部对比，后者变异概率大，收敛也相对快许多。

    3. 交叉变异概率变大会导致种群不稳定。上图3和20对比，可以看到20虽然很快遇到更好的个体。但是种群很不稳定，最优解无法维持下去，种群平均适应度很低。后面74-81虽然结果很好，但也有相同问题。

      根据以上分析，可以得出一个结论，在背包问题情况下，对于种群平均适应度要求不高，当种群最佳适应度和平均适应度保持一定距离时，结果会更好。

  3. 交叉变异方法对比。

    附件中第二部分的实验结果采用的交叉，变异方法是基因的位置为每一个都随机选择，根据实验结果可以看出效果整体都很差，种群不稳定，收敛速度也慢。

  4. 交叉个体选择方法

    附件中第三部分为实验数据，交叉个体的选择方法是顺序选取，这个使得种群更加稳定一定，相比于前者，他更适合于交叉变异概率较小的，收敛速度较慢。

三、旅行商问题实验分析

实验设计

1
2
3
4
5
6
7
8
9
10
11
static double[] mutatePs = {0.02,0.025,0.35};
static double[] crossPs = {0.065,0.075,0.85};
static int[] scales = {4000,5000,6000};
for (int i = 0; i < crossPs.length; i++) {
		for (int j = 0; j < mutatePs.length; j++) {
			for (int j2 = 0; j2 < scales.length; j2++) {
				doTrain(crossPs[i], mutatePs[j],
						scales[j2], 18000);
			}
		}
	}

实验设计就像如上代码所示，分别以一定的区间来跑完所有的测试，然后将每组测试输入的到对应的文件中。实验跑完之后，对实验结果进行分析，然后缩小区间再进行实验。上述代码为调整后的小区间，全部实验见附件第5部分。

实验输出模式

实验过程中每隔300代输出一次，模式如下：

1
2
// 当前代数，当前代最佳适应度，当前代平均适应度，所有代中最佳适应度（适应度为路径长度的倒数）
g: 17701,best: 0.002321846556641697,average: 0.0021039901608931526,best in total: 0.0023259620846458728

最终会输出最佳个体，以及最佳个体最早出现的代数

1
2
// 代数：适应度，个体编码
17089:429.9296220695918,47 22 6 42 23 13 24 12 40 39 18 41 43 14 44 32 38 9 48 8 29 33 49 20 28 15 1 19 34 35 2 27 30 25 7 21 0 31 10 37 4 36 16 3 17 46 11 45 50 26 5

实验结果分析

实验结果从以下角度来衡量

  1. 最佳个体适应度：参数优良性
  2. 最佳个体最早出现代数：收敛速度
  3. 最终几代最佳适应度和平均适应度：参数对种群特征的影响。

实验参数会从种群规模，交叉概率，变异概率，交叉变异算法来分析，实验结果见附件部分，具体分析如下

以下结果默认是随机选择交叉个体，具体的交叉变异方法为前述默认方法。最佳个体适应度是路径长度，而后面最终代最高/平均适应度是路径长度的倒数。

  1. 种群规模影响

    | 实验序号 | 交叉概率 | 变异概率 | 种群规模 | 最佳最早出现代数 | 最佳个体适应度 | 最终代最高/平均适应度 |
    | :——: | :——: | :——: | :——: | :————–: | :————: | :——————-: |
    | 10 | 0.06 | 0.03 | 1000 | 13507 | 445.50 | 0.0022/0.0020 |
    | 11 | 0.06 | 0.03 | 2500 | 11020 | 445.39 | 0.0022/0.0020 |
    | 12 | 0.06 | 0.03 | 500 | 17860 | 476.76 | 0.0020/0.0018 |
    | 13 | 0.06 | 0.03 | 5000 | 15618 | 435.16 | 0.0022/0.0021 |

    从以上数据四组对比分析（更多数据参考附件第四部分），可得

    1. 种群规模较大的5000每次都取得最好的结果，种群规模最小的500效果最差也最慢。
    2. 种群规模大会导致训练速度变慢。

  2. 交叉变异概率的影响

    | 实验序号 | 交叉概率 | 变异概率 | 种群规模 | 最佳最早出现代数 | 最佳个体适应度 | 最终代最高/平均适应度 |
    | :——: | :——: | :——: | :——: | :————–: | :————: | :——————-: |
    | 71 | 0.15 | 0.3 | 1000 | 563 | 946.01 | 8.2668/6.9977 |
    | 72 | 0.15 | 0.3 | 2500 | 16398 | 842.64 | 9.7658/7.7972 |
    | 73 | 0.15 | 0.3 | 500 | 13847 | 976.77 | 8.3581/7.1739 |
    | 103 | 0.85 | 0.025 | 4000 | 9200 | 1080.3 | 7.6112/6.1638 |
    | 104 | 0.85 | 0.025 | 5000 | 16642 | 1093.1 | 7.7736/6.1849 |
    | 105 | 0.85 | 0.025 | 6000 | 11123 | 1112.4 | 7.6321/6.1895 |
    | 4 | 0.065 | 0.02 | 4000 | 17088 | 446.83 | 0.0021/0.0020 |
    | 5 | 0.065 | 0.02 | 5000 | 17537 | 435.80 | 0.0022/0.0020 |
    | 6 | 0.065 | 0.02 | 6000 | 12531 | 442.49 | 0.0022/0.0020 |
    | 22 | 0.075 | 0.025 | 4000 | 13851 | 446.72 | 0.0022/0.0020 |
    | 23 | 0.075 | 0.025 | 5000 | 17823 | 445.51 | 0.0022/0.0019 |
    | 24 | 0.075 | 0.025 | 6000 | 17089 | 429.92 | 0.0023/0.0021 |

    根据上表数据可得

    1. 首先TSP问题没有前述背包问题所说的，无法跳出初始值的问题。
    2. 与背包问题不同，TSP问题更适合较小的交叉变异概率，当种群很稳定的时候才更容易得到更好的解
    3. 交叉变异概率对收敛速度的影响不显著。
      由以上分析，旅行商问题再训练过程中要保持大量的优良个体才能很好进化。从分析数据来看平均适应度总是与最佳适应度很接近。

  3. 交叉变异方法对比。

    这一点没有实现多终交叉变异方法，暂时没有数据。

  4. 交叉个体选择方法
    附件第五部分为顺序选择交叉个体的方法，换用这种方法影响不是很显著，同样要求较小的交叉变异概率。性能略差一点。

四、附实验结果

1. 背包问题，随机选择交叉个体算法；交叉变异基因为连续一段

实验序号 交叉概率 变异概率 种群规模 最佳最早出现代数 最佳个体适应度 最终代最高/平均适应度
1 0.3 0.05 1000 4985 101.39 96.599/91.689
2 0.3 0.05 1500 6039 104.69 102.99/98.249
3 0.3 0.05 500 7199 103.29 99.399/95.099
4 0.3 0.15 1000 5167 104.69 103.39/88.305
5 0.3 0.15 1500 2543 106.29 104.69/87.514
6 0.3 0.15 500 5384 106.29 104.79/85.406
7 0.3 0.1 1000 5313 105.79 104.29/92.617
8 0.3 0.1 1500 0 1.0E-1 1.0E-1/9.9999
9 0.3 0.1 500 9992 103.09 100.39/89.534
10 0.3 0.2 1000 5965 106.29 106.29/85.317
11 0.3 0.2 1500 636 106.29 106.29/85.634
12 0.3 0.2 500 8019 105.79 103.29/81.738
13 0.3 0.3 1000 9397 106.29 103.19/72.396
14 0.3 0.3 1500 2860 106.29 106.29/71.079
15 0.3 0.3 500 419 106.29 106.29/75.727
16 0.3 0.5 1000 4934 106.29 101.69/56.033
17 0.3 0.5 1500 1759 106.29 102.49/55.495
18 0.3 0.5 500 5568 106.29 99.699/58.009
19 0.3 0.8 1000 8131 103.39 93.5,a/39.687
20 0.3 0.8 1500 2565 106.29 95.399/38.583
21 0.3 0.8 500 4590 102.89 88.099/39.505
22 0.5 0.05 1000 4222 106.29 103.99/98.414
23 0.5 0.05 1500 0 1.0E-1 1.0E-1/9.9999
24 0.5 0.05 500 0 1.0E-1 1.0E-1/1.0000
25 0.5 0.15 1000 6060 106.29 104.79/87.962
26 0.5 0.15 1500 2571 106.29 102.89/86.541
27 0.5 0.15 500 1542 104.6, 103.1,/89.511
28 0.5 0.1 1000 3938 104.79 103.29/93.434
29 0.5 0.1 1500 4393 106.29 106.29/94.621
30 0.5 0.1 500 0 1.0E-1 1.0E-1/1.0000
31 0.5 0.2 1000 7809 106.29 106.29/85.163
32 0.5 0.2 1500 3757 104.69 103.39/82.550
33 0.5 0.2 500 2265 106.29 106.29/83.629
34 0.5 0.3 1000 7812 106.29 106.29/73.506
35 0.5 0.3 1500 1536 106.29 106.29/71.245
36 0.5 0.3 500 0 1.0E-1 1.0E-1/1.0000
37 0.5 0.5 1000 2948 106.29 100.29/55.762
38 0.5 0.5 1500 1235 106.29 100.79/57.799
39 0.5 0.5 500 3052 106.29 98.499/58.568
40 0.5 0.8 1000 9313 104.79 96.599/41.264
41 0.5 0.8 1500 8394 104.79 97.399/40.271
42 0.5 0.8 500 9418 103.69 97.399/37.026
43 0.7 0.05 1000 0 1.0E-1 1.0E-1/9.9999
44 0.7 0.05 1500 0 1.0E-1 1.0E-1/9.9999
45 0.7 0.05 500 0 1.0E-1 1.0E-1/1.0000
46 0.7 0.15 1000 1389 106.29 104.29/88.335
47 0.7 0.15 1500 6355 104.69 103.39/85.504
48 0.7 0.15 500 0 1.0E-1 1.0E-1/1.0000
49 0.7 0.1 1000 9427 102.89 101.99/91.870
50 0.7 0.1 1500 1553 106.29 104.79/94.321
51 0.7 0.1 500 0 1.0E-1 1.0E-1/1.0000
52 0.7 0.2 1000 2405 106.29 106.29/85.934
53 0.7 0.2 1500 1403 106.29 106.29/85.484
54 0.7 0.2 500 2526 106.29 106.29/85.170
55 0.7 0.3 1000 696 106.29 104.6,/73.263
56 0.7 0.3 1500 6709 106.29 106.29/73.064
57 0.7 0.3 500 3546 106.29 105.79/73.133
58 0.7 0.5 1000 2175 106.29 101.49/54.312
59 0.7 0.5 1500 2247 106.29 98.699/54.269
60 0.7 0.5 500 8570 106.29 97.699/56.563
61 0.7 0.8 1000 3233 103.89 95.599/39.389
62 0.7 0.8 1500 4964 105.79 94.099/39.547
63 0.7 0.8 500 4966 104.79 95.599/36.744
64 0.85 0.05 1000 0 1.0E-1 1.0E-1/9.9999
65 0.85 0.05 1500 6533 101.6 97.5,a/92.037
66 0.85 0.05 500 0 1.0E-1 1.0E-1/1.0000
67 0.85 0.15 1000 6378 106.29 106.29/88.827
68 0.85 0.15 1500 1306 106.29 105.79/89.643
69 0.85 0.15 500 3931 106.29 106.29/89.689
70 0.85 0.1 1000 6697 104.79 103.29/93.269
71 0.85 0.1 1500 2893 106.29 103.99/93.249
72 0.85 0.1 500 2996 104.6, 103.1,/92.126
73 0.85 0.2 1000 3235 106.29 106.29/82.733
74 0.85 0.2 1500 351 106.29 106.29/82.617
75 0.85 0.2 500 0 1.0E-1 1.0E-1/1.0000
76 0.85 0.3 1000 569 106.29 104.79/69.521
77 0.85 0.3 1500 386 106.29 104.59/71.282
78 0.85 0.3 500 6896 106.29 104.79/72.296
79 0.85 0.5 1000 2752 106.29 103.09/56.570
80 0.85 0.5 1500 340 106.29 101.89/56.360
81 0.85 0.5 500 6702 106.29 94.599/54.731
82 0.85 0.8 1000 3644 104.79 96.999/38.306
83 0.85 0.8 1500 4584 106.29 93.399/39.997
84 0.85 0.8 500 8873 103.29 93.4/35.783

2. 背包问题，随机选择交叉个体算法；交叉变异基因为随机选择的

实验序号 交叉概率 变异概率 种群规模 最佳最早出现代数 最佳个体适应度 最终代最高/平均适应度
1 0.3 0.05 1000 2227 102.3 92.699/88.606
2 0.3 0.05 1500 4206 102.29 91.0/86.834
3 0.3 0.05 500 4652 86.899 74.0,a/68.711
4 0.3 0.15 1000 4382 88.899 75.6,a/62.574
5 0.3 0.15 1500 2371 101.49 86.899/72.841
6 0.3 0.15 500 5905 103.89 97.999/83.583
7 0.3 0.1 1000 4908 99.699 89.499/80.327
8 0.3 0.1 1500 9488 104.69 101.29/91.262
9 0.3 0.1 500 5898 101.39 88.5,a/79.481
10 0.3 0.2 1000 613 106.29 104.79/86.058
11 0.3 0.2 1500 1099 102.59 98.099/79.895
12 0.3 0.2 500 4164 100.29 90.5,a/73.228
13 0.3 0.3 1000 4133 103.59 101.49/71.145
14 0.3 0.3 1500 668 106.29 106.29/74.033
15 0.3 0.3 500 762 106.29 101.79/72.667
16 0.3 0.5 1000 1335 106.29 101.69/53.328
17 0.3 0.5 1500 1692 106.29 103.99/53.314
18 0.3 0.5 500 1175 106.29 103.79/52.869
19 0.3 0.8 1000 273 106.29 100.89/21.714
20 0.3 0.8 1500 1640 106.29 101.89/19.128
21 0.3 0.8 500 9036 106.29 100.39/20.058
22 0.5 0.05 1000 5506 81.4,0 59.2,a/56.048
23 0.5 0.05 1500 9556 92.399 75.999/64.312
24 0.5 0.05 500 9958 90.499 74.8,a/70.312
25 0.5 0.15 1000 6274 95.699 88.0,a/73.908
26 0.5 0.15 1500 1319 91.899 81.999/65.415
27 0.5 0.15 500 7669 97.6,0 88.599/77.501
28 0.5 0.1 1000 7911 95.599 82.199/74.228
29 0.5 0.1 1500 9143 98.599 74.799/67.240
30 0.5 0.1 500 8097 97.799 84.8,a/73.737
31 0.5 0.2 1000 6718 103.49 99.999/80.305
32 0.5 0.2 1500 7884 94.1,0 84.699/67.193
33 0.5 0.2 500 4296 103.79 99.599/80.246
34 0.5 0.3 1000 1233 104.79 101.89/69.945
35 0.5 0.3 1500 894 106.29 103.59/72.517
36 0.5 0.3 500 6754 101.39 95.699/67.157
37 0.5 0.5 1000 1473 106.29 106.29/55.273
38 0.5 0.5 1500 9653 105.79 103.19/50.581
39 0.5 0.5 500 1426 106.29 105.79/50.664
40 0.5 0.8 1000 1196 106.29 102.3,/19.792
41 0.5 0.8 1500 1485 106.29 102.29/20.401
42 0.5 0.8 500 773 106.29 101.49/23.543
43 0.7 0.05 1000 1652 89.099 72.399/65.661
44 0.7 0.05 1500 1637 89.6,0 75.300/66.431
45 0.7 0.05 500 7170 75.7,0 57.5,a/53.299
46 0.7 0.15 1000 5089 98.999 88.9,a/70.745
47 0.7 0.15 1500 8045 94.1,0 78.8,a/62.290
48 0.7 0.15 500 6351 87.8,0 68.5,a/57.397
49 0.7 0.1 1000 7342 98.899 89.799/80.907
50 0.7 0.1 1500 6410 101.89 94.199/86.834
51 0.7 0.1 500 6860 87.799 71.999/60.879
52 0.7 0.2 1000 2412 104.59 94.399/76.778
53 0.7 0.2 1500 1293 106.29 101.69/82.088
54 0.7 0.2 500 7535 92.399 76.999/63.471
55 0.7 0.3 1000 2445 100.89 93.899/60.903
56 0.7 0.3 1500 2625 103.69 100.29/70.770
57 0.7 0.3 500 5596 100.29 90.999/62.727
58 0.7 0.5 1000 2253 106.29 103.99/53.481
59 0.7 0.5 1500 1602 106.29 101.49/50.137
60 0.7 0.5 500 427 106.29 103.79/53.504
61 0.7 0.8 1000 1078 106.29 101.1,/19.991
62 0.7 0.8 1500 1887 106.29 98.499/19.363
63 0.7 0.8 500 1689 106.29 96.1,a/20.355
64 0.85 0.05 1000 8871 77.1,0 53.699/51.248
65 0.85 0.05 1500 5625 86.199 65.5,a/57.612
66 0.85 0.05 500 6158 84.6,0 55.099/52.775
67 0.85 0.15 1000 8047 97.999 81.6,a/69.476
68 0.85 0.15 1500 1810 90.999 64.0,a/53.601
69 0.85 0.15 500 9666 98.599 79.6,a/67.560
70 0.85 0.1 1000 9543 102.49 89.299/79.724
71 0.85 0.1 1500 9313 96.799 82.299/70.985
72 0.85 0.1 500 4771 79.7,0 50.6/46.549
73 0.85 0.2 1000 9374 89.799 66.999/54.277
74 0.85 0.2 1500 4280 99.199 89.6/72.226
75 0.85 0.2 500 5548 83.699 61.8/45.642
76 0.85 0.3 1000 8296 99.899 93.199/62.980
77 0.85 0.3 1500 530 99.799 89.899/60.062
78 0.85 0.3 500 4178 100.79 85.799/59.842
79 0.85 0.5 1000 2748 105.79 102.99/48.664
80 0.85 0.5 1500 375 106.29 106.29/53.665
81 0.85 0.5 500 3256 106.29 106.29/55.009
82 0.85 0.8 1000 1076 106.29 100.79/18.212
83 0.85 0.8 1500 1026 106.29 99.799/17.357
84 0.85 0.8 500 3547 106.29 98.799/19.219

3. 背包问题，顺序选择交叉个体算法；交叉变异基因为连续一段

实验序号 交叉概率 变异概率 种群规模 最佳最早出现代数 最佳个体适应度 最终代最高/平均适应度
1 0.3 0.05 1000 0 1.0E-1 1.0E-1/9.9999
2 0.3 0.05 1500 0 1.0E-1 1.0E-1/9.9999
3 0.3 0.05 500 0 1.0E-1 1.0E-1/1.0000
4 0.3 0.15 1000 3760 106.29 106.29/91.432
5 0.3 0.15 1500 597 106.29 106.29/91.369
6 0.3 0.15 500 7026 106.29 106.29/89.787
7 0.3 0.1 1000 3378 104.69 103.39/92.859
8 0.3 0.1 1500 3839 106.29 106.29/96.837
9 0.3 0.1 500 0 1.0E-1 1.0E-1/1.0000
10 0.3 0.2 1000 3291 106.29 106.29/85.683
11 0.3 0.2 1500 3984 106.29 106.29/84.381
12 0.3 0.2 500 6216 106.29 106.29/82.546
13 0.3 0.3 1000 4993 106.29 104.79/73.038
14 0.3 0.3 1500 4880 106.29 106.29/71.597
15 0.3 0.3 500 0 1.0E-1 1.0E-1/1.0000
16 0.3 0.5 1000 3322 106.29 97.799/55.437
17 0.3 0.5 1500 2144 106.29 102.29/56.235
18 0.3 0.5 500 484 106.29 101.09/54.627
19 0.3 0.8 1000 4542 104.1, 92.1,a/39.286
20 0.3 0.8 1500 2619 106.29 92.7,a/40.538
21 0.3 0.8 500 4261 105.79 88.899/37.666
22 0.5 0.05 1000 0 1.0E-1 1.0E-1/9.9999
23 0.5 0.05 1500 7742 104.29 103.29/98.806
24 0.5 0.05 500 0 1.0E-1 1.0E-1/1.0000
25 0.5 0.15 1000 4001 106.29 106.29/91.453
26 0.5 0.15 1500 2323 105.79 104.69/88.914
27 0.5 0.15 500 0 1.0E-1 1.0E-1/1.0000
28 0.5 0.1 1000 5872 106.29 106.29/93.651
29 0.5 0.1 1500 681 106.29 106.29/95.037
30 0.5 0.1 500 0 1.0E-1 1.0E-1/1.0000
31 0.5 0.2 1000 4985 106.29 106.29/83.875
32 0.5 0.2 1500 8047 106.29 104.79/82.026
33 0.5 0.2 500 631 106.29 106.29/84.867
34 0.5 0.3 1000 5875 106.29 102.59/72.934
35 0.5 0.3 1500 5946 106.29 106.29/73.111
36 0.5 0.3 500 0 1.0E-1 1.0E-1/1.0000
37 0.5 0.5 1000 4691 106.29 101.09/55.391
38 0.5 0.5 1500 1791 106.29 102.29/57.943
39 0.5 0.5 500 4664 105.79 99.899/57.756
40 0.5 0.8 1000 9308 103.79 91.099/37.646
41 0.5 0.8 1500 7539 105.79 98.899/38.566
42 0.5 0.8 500 6502 105.79 89.699/36.866
43 0.7 0.05 1000 4050 101.09 97.799/92.741
44 0.7 0.05 1500 1198 106.29 106.29/100.62
45 0.7 0.05 500 0 1.0E-1 1.0E-1/1.0000
46 0.7 0.15 1000 661 106.29 106.29/90.585
47 0.7 0.15 1500 3500 106.29 106.29/90.165
48 0.7 0.15 500 0 1.0E-1 1.0E-1/1.0000
49 0.7 0.1 1000 5052 104.29 101.49/90.294
50 0.7 0.1 1500 956 106.29 104.79/92.021
51 0.7 0.1 500 0 1.0E-1 1.0E-1/1.0000
52 0.7 0.2 1000 1151 106.29 106.29/84.617
53 0.7 0.2 1500 1275 106.29 106.29/85.197
54 0.7 0.2 500 5786 106.29 106.29/84.322
55 0.7 0.3 1000 3680 106.29 103.39/70.758
56 0.7 0.3 1500 1595 106.29 106.29/72.647
57 0.7 0.3 500 2139 106.29 103.69/73.611
58 0.7 0.5 1000 2154 106.29 101.99/59.084
59 0.7 0.5 1500 6718 106.29 103.09/56.684
60 0.7 0.5 500 5024 106.29 97.599/50.578
61 0.7 0.8 1000 6387 106.29 96.599/40.926
62 0.7 0.8 1500 7798 104.6, 96.6,a/39.596
63 0.7 0.8 500 9081 104.69 88.999/35.515
64 0.85 0.05 1000 5029 104.29 100.69/93.158
65 0.85 0.05 1500 9738 103.99 103.49/96.426
66 0.85 0.05 500 0 1.0E-1 1.0E-1/1.0000
67 0.85 0.15 1000 6507 106.29 103.79/89.389
68 0.85 0.15 1500 7129 106.29 104.79/87.170
69 0.85 0.15 500 951 106.29 106.29/88.782
70 0.85 0.1 1000 669 106.29 106.29/95.184
71 0.85 0.1 1500 9196 106.29 103.19/92.961
72 0.85 0.1 500 2571 106.29 106.29/95.421
73 0.85 0.2 1000 4645 106.29 106.29/82.197
74 0.85 0.2 1500 1898 106.29 106.29/84.104
75 0.85 0.2 500 7453 106.29 105.79/81.303
76 0.85 0.3 1000 3455 106.29 103.59/69.239
77 0.85 0.3 1500 1919 106.29 106.29/73.412
78 0.85 0.3 500 2854 106.29 104.59/72.612
79 0.85 0.5 1000 2615 106.29 99.799/54.608
80 0.85 0.5 1500 1341 106.29 100.79/54.746
81 0.85 0.5 500 4064 106.29 100.49/58.421
82 0.85 0.8 1000 2942 103.99 94.499/38.860
83 0.85 0.8 1500 6671 103.99 93.3,a/40.284
84 0.85 0.8 500 7575 103.99 91.499/38.636

4. 旅行商问题，随机选择交叉个体，交叉变异方法默认

实验序号 交叉概率 变异概率 种群规模 最佳最早出现代数 最佳个体适应度 最终代最高/平均适应度
1 0.065 0.025 4000 14614 443.69 0.0022/0.0020
2 0.065 0.025 5000 14829 432.23 0.0022/0.0020
3 0.065 0.025 6000 10241 456.18 0.0021/0.0019
4 0.065 0.02 4000 17088 446.83 0.0021/0.0020
5 0.065 0.02 5000 17537 435.80 0.0022/0.0020
6 0.065 0.02 6000 12531 442.49 0.0022/0.0020
7 0.065 0.35 4000 12893 749.35 0.0010/8.0311
8 0.065 0.35 5000 9315 739.86 0.0010/8.5105
9 0.065 0.35 6000 10414 775.17 0.0011/8.4818
10 0.06 0.03 1000 13507 445.50 0.0022/0.0020
11 0.06 0.03 2500 11020 445.39 0.0022/0.0020
12 0.06 0.03 500 17860 476.76 0.0020/0.0018
13 0.06 0.03 5000 15618 435.16 0.0022/0.0021
14 0.06 0.06 1000 17913 459.77 0.0021/0.0018
15 0.06 0.06 2500 16826 441.73 0.0022/0.0019
16 0.06 0.06 500 17501 515.00 0.0018/0.0016
17 0.06 0.06 5000 17747 434.56 0.0022/0.0020
18 0.06 0.08 1000 14049 446.96 0.0021/0.0018
19 0.06 0.08 2500 15902 439.36 0.0022/0.0019
20 0.06 0.08 500 16238 545.68 0.0016/0.0014
21 0.06 0.08 5000 17836 440.37 0.0022/0.0019
22 0.075 0.025 4000 13851 446.72 0.0022/0.0020
23 0.075 0.025 5000 17823 445.51 0.0022/0.0019
24 0.075 0.025 6000 17089 429.92 0.0023/0.0021
25 0.075 0.02 4000 17476 441.52 0.0022/0.0020
26 0.075 0.02 5000 15679 438.29 0.0022/0.0020
27 0.075 0.02 6000 17477 442.60 0.0022/0.0020
28 0.075 0.35 4000 7528 783.76 0.0010/8.1426
29 0.075 0.35 5000 8132 763.77 0.0012/8.9255
30 0.075 0.35 6000 17917 760.50 0.0011/8.6827
31 0.08 0.03 1000 17634 473.58 0.0020/0.0018
32 0.08 0.03 2500 16047 446.92 0.0021/0.0019
33 0.08 0.03 500 17943 463.33 0.0021/0.0018
34 0.08 0.03 5000 12038 430.88 0.0023/0.0020
35 0.08 0.06 1000 16924 445.96 0.0022/0.0018
36 0.08 0.06 2500 17732 432.16 0.0022/0.0020
37 0.08 0.06 500 7864 599.34 0.0014/0.0012
38 0.08 0.06 5000 15750 437.94 0.0022/0.0019
39 0.08 0.08 1000 17349 465.93 0.0020/0.0017
40 0.08 0.08 2500 10728 455.08 0.0021/0.0018
41 0.08 0.08 500 16878 586.23 0.0014/0.0012
42 0.08 0.08 5000 9275 445.36 0.0022/0.0019
43 0.12 0.03 1000 17857 449.05 0.0022/0.0019
44 0.12 0.03 2500 14048 440.42 0.0022/0.0019
45 0.12 0.03 500 11996 545.93 0.0012/0.0011
46 0.12 0.03 5000 12799 438.78 0.0022/0.0019
47 0.12 0.06 1000 17770 520.20 0.0018/0.0015
48 0.12 0.06 2500 17336 457.30 0.0021/0.0017
49 0.12 0.06 500 17307 683.22 0.0012/0.0010
50 0.12 0.06 5000 10160 448.12 0.0022/0.0018
51 0.12 0.08 1000 8671 559.33 0.0015/0.0012
52 0.12 0.08 2500 13787 436.80 0.0022/0.0018
53 0.12 0.08 500 17679 740.26 0.0011/9.6734
54 0.12 0.08 5000 11571 441.66 0.0022/0.0018
55 0.15 0.05 1000 17570 552.99 0.0016/0.0013
56 0.15 0.05 2500 17395 451.57 0.0022/0.0017
57 0.15 0.05 500 2479 752.13 0.0010/9.0707
58 0.15 0.05 5000 9550 444.93 0.0022/0.0018
59 0.15 0.15 1000 16207 816.78 0.0010/8.4039
60 0.15 0.15 2500 7308 663.57 0.0011/9.2080
61 0.15 0.15 500 10509 867.26 9.7517/7.8680
62 0.15 0.15 5000 4906 575.47 0.0015/0.0011
63 0.15 0.1 1000 5753 712.81 0.0011/9.6629
64 0.15 0.1 2500 16068 543.71 0.0017/0.0013
65 0.15 0.1 500 2746 656.60 0.0010/8.3858
66 0.15 0.1 5000 14404 435.66 0.0021/0.0016
67 0.15 0.2 1000 16145 847.45 9.5506/7.7630
68 0.15 0.2 2500 6435 763.46 0.0011/8.8676
69 0.15 0.2 500 3560 931.15 9.4965/7.8220
70 0.15 0.2 5000 10484 686.18 0.0012/9.5366
71 0.15 0.3 1000 563 946.01 8.2668/6.9977
72 0.15 0.3 2500 16398 842.64 9.7658/7.7972
73 0.15 0.3 500 13847 976.77 8.3581/7.1739
74 0.15 0.3 5000 14262 818.78 0.0010/7.7550
75 0.1 0.05 1000 16415 458.54 0.0021/0.0018
76 0.1 0.05 2500 17757 449.22 0.0022/0.0019
77 0.1 0.05 500 17776 511.99 0.0018/0.0016
78 0.1 0.05 5000 7574 439.92 0.0022/0.0019
79 0.1 0.15 1000 7280 717.19 0.0011/9.5669
80 0.1 0.15 2500 17861 566.03 0.0016/0.0013
81 0.1 0.15 500 8327 799.33 0.0010/8.9440
82 0.1 0.15 5000 16136 440.13 0.0022/0.0017
83 0.1 0.1 1000 7140 527.27 0.0014/0.0012
84 0.1 0.1 2500 16904 458.82 0.0021/0.0017
85 0.1 0.1 500 7663 720.98 0.0011/9.5457
86 0.1 0.1 5000 16178 438.59 0.0022/0.0018
87 0.1 0.2 1000 8091 783.17 9.8503/8.2363
88 0.1 0.2 2500 3862 692.41 0.0012/9.3888
89 0.1 0.2 500 15881 850.45 9.6596/8.1267
90 0.1 0.2 5000 12757 565.44 0.0014/0.0011
91 0.1 0.3 1000 12445 874.03 9.6724/7.8296
92 0.1 0.3 2500 16123 810.13 0.0010/7.9321
93 0.1 0.3 500 14625 924.36 9.0194/7.5651
94 0.1 0.3 5000 13230 674.58 0.0010/7.8925
95 0.1 0.5 1000 9504 908.99 8.9805/6.9308
96 0.1 0.5 2500 16516 949.85 9.0347/6.9883
97 0.1 0.5 500 6073 991.62 8.5611/6.9454
98 0.1 0.5 5000 3240 915.21 9.1122/6.9476
99 0.1 0.8 1000 8494 1007.8 7.6070/6.5249
100 0.1 0.8 2500 9774 1019.6 8.2451/6.5762
101 0.1 0.8 500 835 1062.1 7.9353/6.6638
102 0.1 0.8 5000 10601 989.88 8.4705/6.6346
103 0.85 0.025 4000 9200 1080.3 7.6112/6.1638
104 0.85 0.025 5000 16642 1093.1 7.7736/6.1849
105 0.85 0.025 6000 11123 1112.4 7.6321/6.1895
106 0.85 0.02 4000 17962 1079.0 8.4245/6.1990
107 0.85 0.02 5000 11666 1075.2 7.7231/6.1773
108 0.85 0.02 6000 9899 1080.4 8.1077/6.1932
109 0.85 0.35 4000 8878 1111.2 7.7423/6.1686
110 0.85 0.35 5000 12532 1072.7 7.5296/6.1738
111 0.85 0.35 6000 9934 1076.6 7.7069/6.1643

5. 旅行商问题，顺序选择交叉个体，交叉变异方法默认

实验序号 交叉概率 变异概率 种群规模 最佳最早出现代数 最佳个体适应度 最终代最高/平均适应度
1 0.065 0.025 4000 10223 440.68 0.0022/0.0020
2 0.065 0.025 5000 11598 436.68 0.0022/0.0021
3 0.065 0.025 6000 17646 434.46 0.0022/0.0020
4 0.065 0.02 4000 17472 454.76 0.0021/0.0020
5 0.065 0.02 5000 17025 443.31 0.0022/0.0020
6 0.065 0.02 6000 9995 443.89 0.0022/0.0020
7 0.065 0.35 4000 11817 774.53 0.0010/8.0710
8 0.065 0.35 5000 11144 769.55 0.0010/8.2835
9 0.065 0.35 6000 11745 748.65 0.0011/8.4933
10 0.075 0.025 4000 16996 445.88 0.0022/0.0020
11 0.075 0.025 5000 17161 438.01 0.0022/0.0020
12 0.075 0.025 6000 10908 449.83 0.0022/0.0019
13 0.075 0.02 4000 16352 436.46 0.0022/0.0020
14 0.075 0.02 5000 16196 442.23 0.0022/0.0020
15 0.075 0.02 6000 10715 437.49 0.0022/0.0020
16 0.075 0.35 4000 9593 727.09 0.0010/7.7911
17 0.075 0.35 5000 9132 795.94 0.0010/8.2917
18 0.075 0.35 6000 14348 812.68 0.0010/8.4874
19 0.85 0.025 4000 6052 1112.8 7.7484/6.1796
20 0.85 0.025 5000 10644 1066.2 7.7750/6.1791
21 0.85 0.025 6000 2473 1091.7 7.7044/6.1711
22 0.85 0.02 4000 1629 1092.2 7.8626/6.1960
23 0.85 0.02 5000 15103 1065.9 7.8524/6.1656
24 0.85 0.02 6000 5232 1113.9 7.7526/6.1754
25 0.85 0.35 4000 6282 1117.8 7.9990/6.1732
26 0.85 0.35 5000 12813 1125.6 7.9161/6.1742
27 0.85 0.35 6000 12483 1059.0 7.7509/6.1608