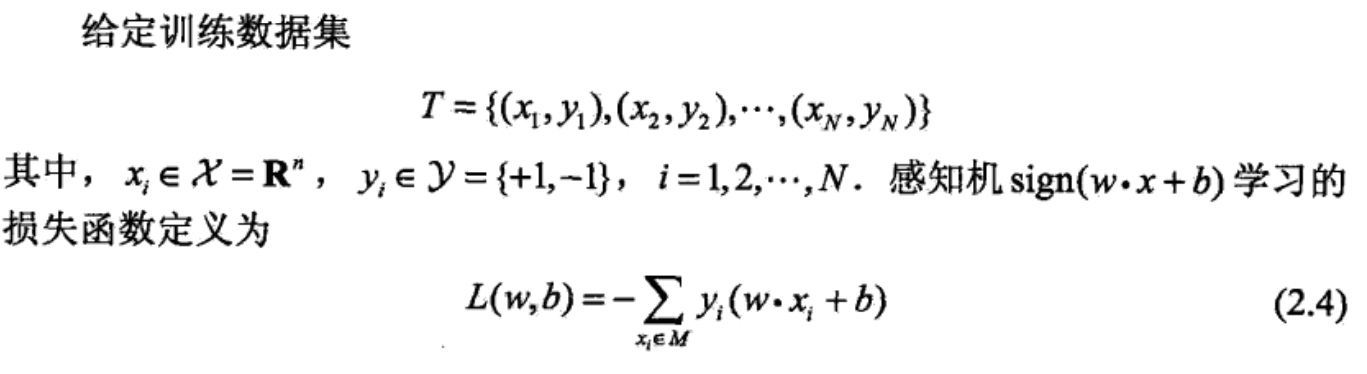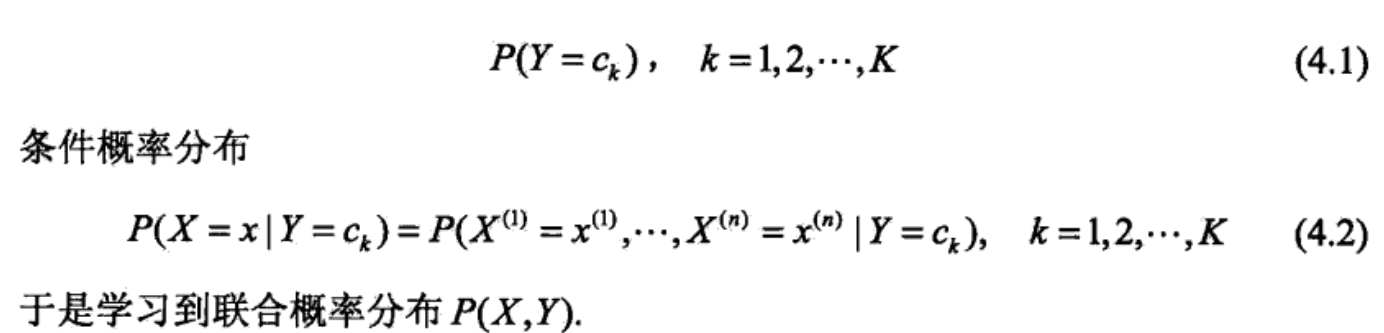1 统计学习概述
统计学习三要素:模型、策略、算法。
1.1 模型
模型就是所要学习的条件概率分布或者决策函数
1.2 策略
策略即是决定用什么样的准则学习或选择最优的模型。
损失函数(loss function)
经验风险最小化和结构风险最小化
- empirical risk minimization,ERM:其理论依据是大数定理。但是通常情况下训练数据较少并不满足大数定理的要求,容易发生过拟合现象。
- structural risk minimization,SRM:为了防止过拟合现象,SRM增加正则化项,对模型的复杂度进行约束,要求模型复杂度较小。
1.3 算法
算法是指学习模型的具体算法,例如BP算法、EM算法等。
1.4 模型评估与模型选择
训练误差、测试误差、交叉验证。
生成模型、判别模型。
2 感知机模型
2.1 模型
$$
f(x) = sign(wx + b) \tag{1.1}
$$
$$
sign(x) = \begin{cases}
1, & \text{if x >= 0} \
-1, & \text{if x < 0}
\end{cases} \tag{1.2}
$$
其中所要训练的参数为w和b,感知机模型是一种简单的线性分类模型,属于判别模型。
2.2 策略
定义 loss function:
2.3 算法
SGD算法:
3 KNN模型
3.1 模型
3.2 策略
KNN模型是一个只需正向统计的过程,没有待训练参数,也不需要定义 loss function 。但是在统计前要决定策略三要素:距离度量方法、k值选择和分类决策方法。
- 距离度量方法: 欧式距离、$L_p$距离、曼哈顿距离等。
- k值选择:k值越小对临近数据点越敏感,模型越复杂,越容易发生过拟合;k值越大,模型越简单,不易发生过拟合,但是模型能力若,预测能力差。
- 分类决策方法:多数表决,平均值方法等。
3.3 算法
最简单的算法就是线性搜索所有数据集,找出K个最近邻。其搜索复杂度为O(n)
优化的算法如kd树算法,搜索复杂度为 O(log n)
构造kd树
利用kd树搜索最近邻


4 朴素贝叶斯方法
4.1 模型
朴素贝叶斯法通过训练数据来学习联合概率分布P(X,Y)。根据$P(X,Y) = P(X|Y)P(Y)$,所以如下图所示,我们可以通过学习Y的先验概率分布和X的条件概率分布来确定X与Y的联合分布。
之后根据前面所说的大数定理,训练数据满足这种分布,之后的新数据也当满足这种分布。至于训练数据不足的问题,也可套用结构风险最小的理论。
但是求解P(X|Y)的发杂度非常高,设X为n维向量,$x_j$有$S_j$个不同的取值,Y有K个不同的取值。那么统计P(X|Y)的复杂度为$K\Pi_{j=1}^{n}Sj$.
为降低复杂度,朴素贝叶斯法做了X的每个维度相互独立的假设,那么条件概率分布变为:
$$
P(X=x|Y=y) = P(X^1=x^1,…,X^n = x^n | Y=c_k) \
= \Pi_{j=1}^nP(X^j = x^j|Y=c_k) \
k = 1,2,…,K \tag{4.3}
$$
这样使得模型变得简单,可计算。但是其效果就要差一点。
4.2 策略
朴素贝叶斯的策略被称为后验概率最大化策略,后面会说明这一策略和经验风险最小化策略是等价的。
后验概率最大化策略
后验概率最大等价于经验风险最小
为了证明这个问题,首先定义0-1损失函数如下:
$$
L(Y,F(X)) = \begin{cases}
1, & Y \neq f(X) \
-1, & Y = f(X)
\end{cases}
$$
式中f(X)式分类决策函数. 这时,期望风险函数为
$$
R_{exp} = E[L(Y,f(X))]
$$
然后利用条件期望全期望公式得:
$$
R_{exp}(f) = E_x\sum_{k=1}^K[L(c_k, f(X))]P(c_k|X)
$$
因为P(X=x)是确定的,所以只需对X=x的情况下逐个取最小化,如下:
$$
\begin{align}
f(x) & = arg {min}{y \in Y}\sum{k=1}^KL(c_k,y)P(c_kX=x) \\
& = arg {min}{y \in Y} \sum{k=1}^KP(y \neq c_k|X=x) \\
& = arg{min}(1-P(y=c_k|X=x)) \\
& = arg {max}_{y \in Y}P(y=c_k|X=x)
\end{align}
$$
这样经验风险最小化就和前面的后验概率最大化策略目标相同了
4.3 算法
5 决策树模型
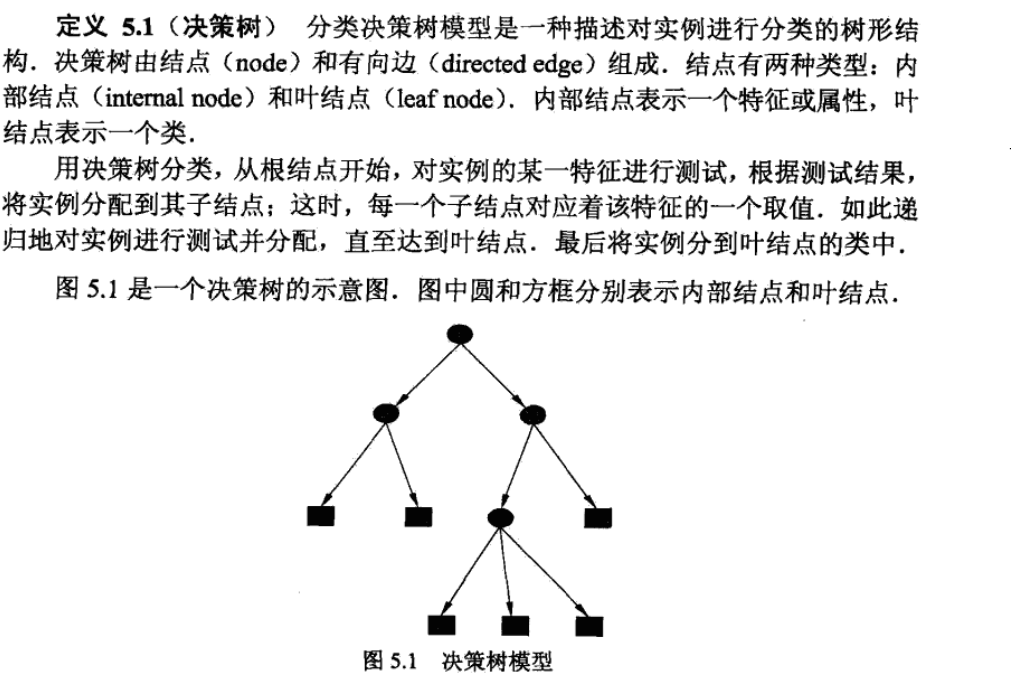
5.1 模型
5.2 策略
决策树的学习策略是损失函数最小的策略,但是这一策略在学习算法中不会明显的体现出来。具体的学习算法只会要求对于训练数据,分类尽可能正确。这也就蕴含了损失函数最小的思想。
即是损失函数已经最小了,决策树学习还要求树的结构最优,即树的层数要尽量少。
5.3 算法
从所有的二叉树中找出结构最优的的树是NP难度的问题。所以具体的算法都是启发式的算法,从根节点开始先找到分类最优的分类特征,然后一次递归地执行下去。
常用的算法有ID3,C4.5 与 CART。这些算法基本都基于信息熵和信息增益的理论。